投稿：师兄有话说之分分钟搞掂矩阵“特征值”要表示什么“特征”

来源：中国数据分析行业网 | 时间：2017-04-07 | 作者：数据委

作者：statist3927——暨南大学金融系，经济学硕士

从很多年前接触到“特征值”这个词开始，我就一直有个疑问没搞明白，为啥矩阵 “特征值”和“特征向量”中的“特征”，与我们日常理解的、一般口语中的“特征”差异怎么就那么大呢？

师兄有话说宣传图 师兄有话说：分分钟搞掂矩阵“特征值”要表示什么“特征”

比方说张飞的“特征”是高大，黑，大胡子……，但矩阵的“特征值”却是：设A是n阶方阵，如果数λ和n维非零列向量x使关系式Ax=λx 成立，那么这样的数λ称为矩阵A的“特征值”。张飞的特征例子和特征值的定义放在一块，真的非常的风马牛不相及！矩阵的“特征值”想要表现矩阵的“特征”是什么？

直到最近我开始留意国外教材中，关于“特征值”的英文单词的“eigenvalue”的词根“eigen”后，最后形成了一把解开我心中这个结的钥匙。Eigen 翻译过来叫做“本征”、“固有的”、“自己的”。在这里，我认为“固有的”、“本征”解释会比“特征”更加贴近原意。在线性代数中，如果将一个向量在空间中展示的话，会有2个“固有”或“本征”的特性，一个是其方向，一个是其长度。一个方阵A左乘一个非零列向量x，往往是表示“将这个向量x进行线性转换”的意思。而转化的过程，就是通过A。举个例子来说，下图，要将向量v转化成向量V，那么就需要改变v的方向，然后拉长其长度。

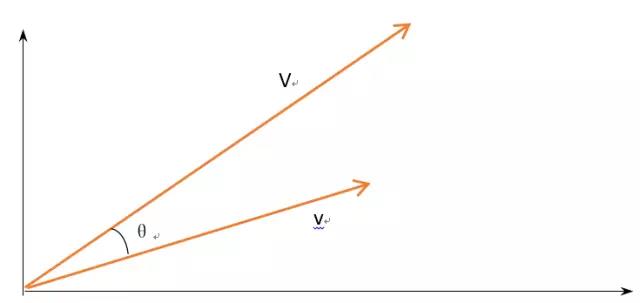师兄有话说示例图那怎么样在矩阵代数中实现呢？过程如下：

师兄有话说示例图1

这个时候回过头来再看看“eigenvalue”和“eigenvector”的定义，我们就能够借鉴上面的转换例子来了解到：这个矩阵A，对向量x进行了转换后，并没有改变其“固有”的方向，却只改变了向量的长度λ倍。所以说，这个时候和向量的“固有”特性、“本征”从语言和逻辑上就扯上关系了，而且还不是牵强附会那种。

为了进一步直观的理解上面的话，我们还是举二维向量的例子吧：

师兄有话说示例图2

用图表示就是：

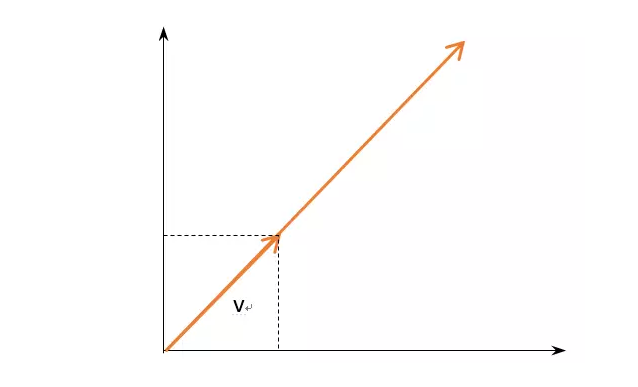
师兄有话说示例图3

综合以上的分析过程看来，“eigenvalue”应该是这样理解：矩阵A在不改变某些向量“固有”方向的基础上，对向量只进行长度λ倍的变换，因此λ就是矩阵A能将这些向量进行保留“本征”变换的倍数值。而“eigenvector”就是矩阵A能够进行这种保留“本征”变换λ倍的那些向量。因此，有些港澳台或者国外翻译的教材，并不把“eigenvalue”翻译成特征值，而是“本征值”，我觉得这么翻译反而更有道理，更贴近原意。

当然了，说到最后，我还是觉得这次解惑的探索过程，应验了某句名言“问题讲清楚了，就解决了一半”。确实，很多求知过程中遇到的问题，理解不了，主要是因为没搞懂“概念”或者没能搞懂确切的含义。当搞清楚或澄清了“是什么”的问题后，问题反而就解决了！

声明：本文为中国商业联合会数据分析专业委员会市场处供稿至数据委会员处，转载请经原作者：statist3927和会员处的允许，否则视为侵权！

上一篇： AI大师吴恩达：数百万人的饭碗很快要被AI抢了

下一篇：手把手教你做数据分析

数据委概述

大事回顾

数据委动态

中国数据分析行业现状

行业介绍

应用实例

技术热点

Datahoop大数据分析平台

解决方案

会员活动

会员服务

入会申请快速指南

行业协会特邀专家

联系我们

中国商业联合会数据分析专业委员会

投稿：师兄有话说之分分钟搞掂矩阵“特征值”要表示什么“特征”