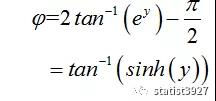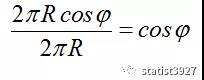(作者:CPDA数据分析师 刘程浩)
前不久我和同事一起瞎聊,聊到制作数据可视化时,有个话题吸引了我的注意:如果不注意纬度的变化,高纬度地区地图上展示的栅格图,会存在因地图变形导致栅格内数据有很大误差的场景。
说者无心,听着有意,这大概就是一杯咖啡汇聚宇宙能量的某个具体表现吧。
说到栅格图,简单科普下,就是为了研究某个地理区域的各项指标分布状况,将该区域用若干的单位面积单元格覆盖,并通过色块的阶梯来呈现指标的分布情况。
例如下图,我采用了某个技术论坛上在百度地图上绘制的上海市区的一个栅格地图
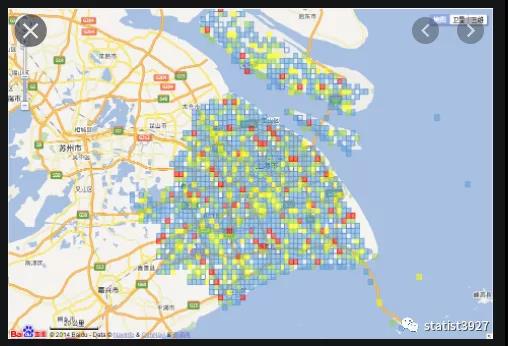
在上面的栅格地图中,每个单元格可以表示1×1km的区域,或N×Nkm的区域。并且每个栅格的颜色由浅到深,可以表示很多指标的高低。例如人口密度、空气PM2.5、用电量……等等。
由于栅格地图具有非常直观的多维地理呈现功能,因此单个栅格地图或多个栅格地图的对比使用,可以从数据中得到非常多的发现。
那我们聊天的话题中,为什么这个话题会这么吸引我呢?原因可能是受我中学时代当过地理课代表的原因吧。
当然了,由于我国国土大部分面积都处于中低纬度,我本次文章题目中出现的问题并不严重(准确的说地图绘制方法不同)。而且我们用栅格地图研究问题时,往往研究的是一个小范围区域,此时的地图变形误差影响并不大,也容易纠正。
但是当我们放眼全球时,特别的,在靠近两级的地方做研究时(例如俄罗斯的远东地区、智利狭长的跨中高纬度国土、阿根廷靠近南极圈区域等等),这种情况就比较明显了。而且由于地图的变形严重,用变形的地图来制作栅格地图,那么就相当站在巨大误差的肩膀上,得到的结果就匪夷所思了。
那,为什么会出现地图变形呢?我们就回到中学地理来看看。
我们生活在地球,假设地球是个正球体。如果我们想把地球表面做成一个平面二维的地图,会发现因为正球体表面无法连续分割,导致做不出一个完整的地图。
另外,仔细观察地球仪,我们会发现高纬度地区,极点、经线和纬线闭合的区域其实是个曲面三角形。
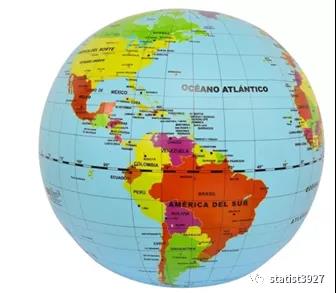
如果按照经线把地球仪表面剥开并铺平,你是无法得到一个连续的地图的。那我们平时看到的世界地图是怎么画出来的?大部分用到的是圆柱投影法(又称墨卡托投影法Mercatorprojection,或麦卡托投影法、正轴等角圆柱投影法)
假设用一张白纸卷成一个圆管,套在一个半透明地球仪上。地球仪的赤道和纸管相切。然后在这个半透明的地球仪中心放一个灯泡,点亮这个灯泡,那么地球仪表面的地图就会投影到这个纸管上面。
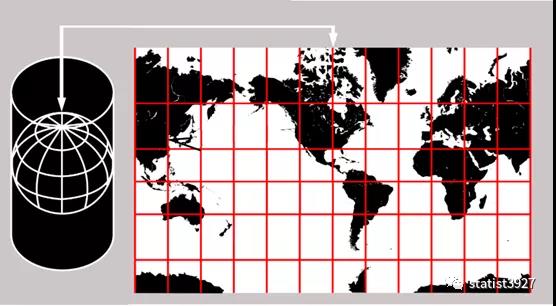
我们把纸管上留下的投影地图展开,就会得到我们常见的世界地图了。
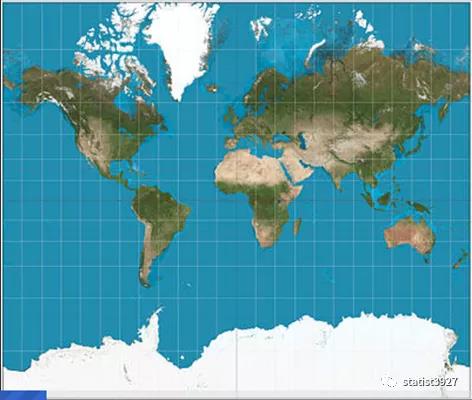
这个世界地图有2个最大的特点:
1、每条纬线都一样长,和实际地球仪上存在较大的出入。因为我们知道纬度越高,纬线圈就越小。
2、纬度越高,投影长度就被拉长的越厉害
这个出入就造成了地图变形。
也就是说,在投影法得到的地图上,纬度越高,看上去一定大小的地区,实际上在地球上是没有那么大的。就好像上图中的南极洲,它横向覆盖了一整条纬线,而我国在世界地图上的大小,才占据了1/6根纬线。而且整体看上去南极洲比我国大的多的多。但实际上南极洲只有1400万平方公里,只比我国大40%左右。同理,靠近北极圈的格陵兰岛,变形后看上去就很大,和南美洲差不多大。但实际上格陵兰岛只有216万平方公里,还不够我国的1/4 !因此,在这个投影法绘制的地图上,特别是高纬度地区实际面积放大了的前提下,用栅格图进行分析,就容易出问题。
以上分析了问题的表现,以及问题的根本成因,那么如何进行修正呢?
我们采用了一个非测绘专业,但符合专业的数据分析师的思维的方法。
利用古德曼函数的逆推导得到面积缩放修正法。
- 1. 古德曼函数简介
纬度实际上是一个球心角,假设不存在地球自转偏转角,赤道平面就是水平面。纬度实际上就是以赤道平面向上或向下的旋转的一个球心角φ。这个球心角所对应的圆弧,在相切的平面上的笛卡尔投影为y。
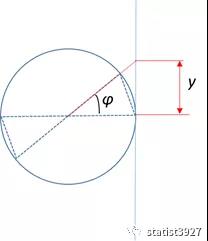
那么地理坐标经纬度(λ,φ)和平面笛卡尔坐标(x,y)之间的关系就如下图
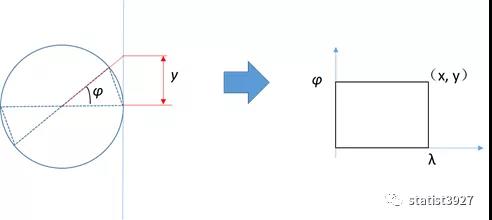
通过古德曼函数的逆运算(也就是反函数),是可以得到纬度φ和地图上的纬度y之间的关系。
这个是古德曼函数
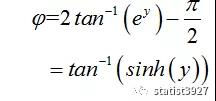
我们做个对比,看看2种数值之间的差异,按地球平均半径6371KM计算
| 纬度 |
纬度至赤道距离KM |
投影地图的放大倍数 |
| 0 |
0 |
1 |
| 15 |
1668 |
1.049 |
| 30 |
3336 |
1.122 |
| 45 |
5004 |
1.258 |
| 60 |
6672 |
1.549 |
| 75 |
8340 |
24.207 |
有了地球仪上的纬度φ和投影地图上的纬度y之间关系后,还不够,还需要考虑经度上的变形。
在这里我们就不搞那么复杂了,用一个简单的几何方法进行近似替代。
假如确定某个纬度φ,那么在这个纬度上的纬线长度肯定比赤道短。
假设地球仪半径为R,纬度φ上的纬线和赤道相比,这个比例很容易算出来
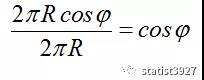
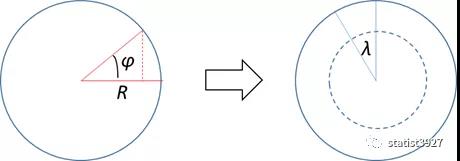
之后就容易估算出地图上一个经纬网格的面积,和地球仪上一个经纬网格的变形比例了。
我们假设地球仪上一个正方形,纬度为15°,经度为15°(考虑每个时区15°的实际业务场景),那么到了投影地图上,面积就会放大。我们把具体的放大倍数做了一个渐进表,如下:
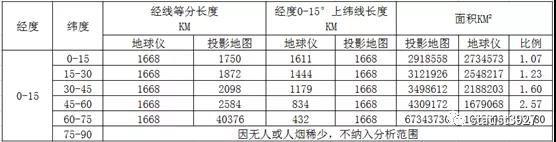
这个表怎么看呢,其实就是看最右边的3列。
例如,在地球仪上0-15°纬度和0-15°经度包围的一个曲面四边形,它的表面积接近2734573km²,而在投影地图上,这个四边形的面积为2918558km²。两者差异不大。也就是说在地球仪上用2734573个1×1km的单元格做栅格,几乎能填满这个区域;而在投影地图上,则需要2918558个单元格。后者是前者的1.07倍。而在高纬度地区,例如60-75°纬度地区,这个比例上升到了接近64倍!所以,当我们用栅格图计算时,会发现高纬度地区的城市用的单元格多了,但是每个单元格下的指标,例如家庭密度一下子就小了很多。这样一来,同样是高纬度城市的市中心,就会造成这里也人烟稀少的情况,和业务实际差异很大。
因此有了这个比例倍数,我们在使用栅格图时,特别是计算总量或者单元格上的指标时,就可以根据城市所在的纬度区域,去缩小或放大相应的倍数。
当然了,地图使用的投影方法不同,我们计算得到的放大或缩小的倍数变化情况也不同,这个需要根据具体情况做调整。